Modules and Cognitive Efficiency

Press the right key for the next slide (or swipe left)

also ...

Press the left key to go backwards (or swipe right)

Press n to toggle whether notes are shown (no equivalent if you don't have a keyboard)

Press m or double tap to see a menu of slides

We can resolve both puzzles by appeal to the idea that there are modular & non-modular mindreading processes. (Cf. physical objects).

modularity

Explain how this works in the case of each puzzle.

*todo* modify the slide to illustrate the solution

modularity requires cognitive efficiency

First, what do I mean by cognitive efficiency.

Some tasks require mental effort.

For example, suppose I ask you to count from one to one hundred omitting each prime number.

This is not the kind of thing most people can do while washing up.

It requires attention, inhibitory control and working memory.

By contrast, many adults can count in the ordinary way from one to one hundred while washing up.

Counting has become routine, habitual.

So much for cognitive efficiency.

Now why suppose that modularity (or core knowledge) requires cognitive efficiency?

To invoke modularity, we need to understand how mindreading could be (i) automatic and (ii) present in pre-linguistic infants with limited working memory & executive function; both (i) and (ii) mean we need to understand how it could be cognitively efficient. (The situation is a bit like this: we want to say you can perceive others mental states; but on the face of it, mental states are exactly the sort of things that are not available to perception.)

How could mindreading ever (but not always) be automatic?

Representing perceptions and beliefs as such---and even merely holding in mind what another believes, where no inference is required---involves a measurable processing cost\citep{apperly:2008_back,apperly:2010_limits}, consumes attention and working memory in fully competent adults,\citealp{Apperly:2009cc, lin:2010_reflexively, McKinnon:2007rr} may require inhibition\citep{bull:2008_role} and makes demands on executive function.\citep{apperly:2004_frontal,samson:2005_seeing}

We saw earlier that mindreading in four year olds and adults is cognitively demanding.

And there's good reason to think that it should be.

If anything should consume scarce cognitive resources ...

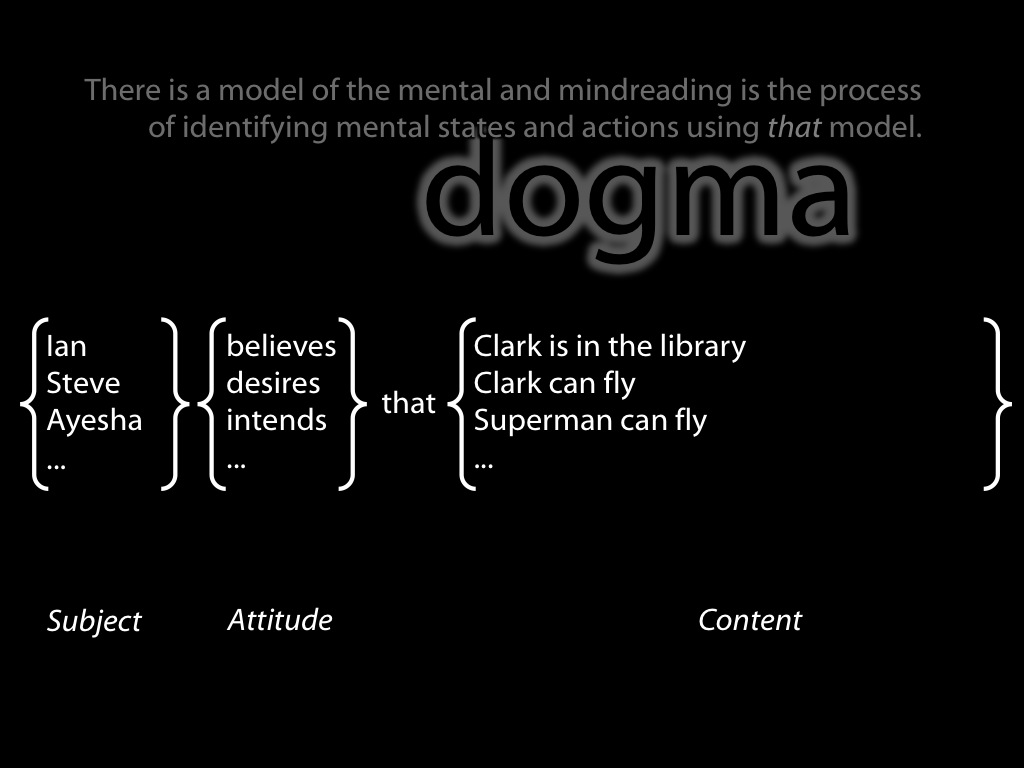
propositional contents

arbitrarily nestable contents

uncodifiably complex causal interactions

attitudes contituted in part by norms

Now appeal to modularity doesn't explain how mindreading might somehow be efficient.

Suppose someone could find prime factors incredibly quickly.

It wouldn't be a satisfying explanation to just say that she had a module for finding prime factors.

We'd also need an algorithm that her module could be implementing consistently with her performance.

So (a) efficiency points to modularity but (b) efficiency requires explanation and (c) gesturing at modularity doesn't explain efficiency.

To see how mindreading could be cognitively efficient, we need to reject a dogma.